オリジナルマシンで「世界」と戦う
今回は、MDGRAPE(エムディーグレープ)という分子動力学シミュレーションを行う専用コンピュータの設計を担う大野さん。よく考えたら MDGRAPEの開発というのは1990年以前からやっているはずで、それってWindows 3.1がようやく出てきたくらいの時代で、今から考えると非常に非力なマシンの時代に開発からやっているって、実はすごいのでは…?ということで、その歴史も含めてお話を聞いてきました。
分子のシミュレーションの専用マシン
MDGRAPEのMDって、分子動力学(Molecular Dynamics)の略だから分子シミュレーションのコンピュータってことですよね。
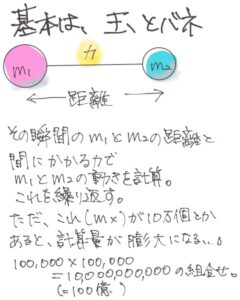
簡単に言うと、原子を玉、原子と原子の間に働く力をバネに見立てて、分子がどういう形になるかとか、分子と分子がどのように相互作用するか、ということをシミュレーションする専用マシンです。
例えば新型コロナウイルスのタンパク質とそれに結合する薬剤の結合をシミュレーションをしたものがあるんですが、これを見ていただくのがわかりやすいですね。
結構ぐるぐる回りますね。
MDシミュレーションしてみるとよくわかるんですが、原子と原子がくっつくといっても、くっつく向きもけっこういろいろあるんです。
この動画では見やすくするためにこういう構造で表示していますけど、アミノ酸の原子を全部一個一個ちゃんと計算しているんです。
時間スケールはどのくらいなんですか?
計算の1ステップが1フェムト秒(fsec、10-15秒=1000兆分の1秒!)で、この動画全体だと1マイクロ秒(μsec、100万分の1秒)くらいの長さですね。この長さでも10億回計算しています。とはいえ、もっと長くやらないと、タンパク質の挙動をシミュレーションするには不十分なんです。
元は天体シミュレーション
MDGRAPEのGRAPEの方は、重力のGravityからですよね。
話は1990年代までさかのぼるんですが、長野県の野辺山の電波天文台にいらっしゃる近田義広先生(現国立天文台名誉教授)から、専用計算機を作れば重力多体問題について計算できるのではないか、という考えが出てきたんです。
多体問題は、いまのところ数値シミュレーションするしかないですからね。
ニュートンの万有引力は無限遠まで影響があるので、例えば星が10億個あったら、10億個の全ペアの間に重力が働いているわけで、理論的には10億個×10億個の組み合わせの重力を一個一個計算しなきゃいけなくなってしまうんです。実際の実用的な計算プログラムでは近似アルゴリズムを使って組み合わせの数を減らしています。だからよく使われるアルゴリズムでは粒子の個数が10倍になっても計算量は二乗の100倍ではなく、30倍程度に収まるんですけどね。でも専用のハードウェアがあれば銀河とか球状星団という星の集団の計算がすごく加速するだろうと提案したんです。その提案を受けて杉本大一郎先生(東京大学教養学部教授、当時)が球状星団の進化の研究に使えると考えて開発に着手しました。重力(GRAvity)の計算式を小分けにして多数の演算回路を並べて流れ作業で計算するパイプライン(PipEline)方式ということでGRAPEと名付けられました。最初は重力のみを対象としていましたが、同じように粒子ペアに働く力を計算する分子動力学シミュレーションにカスタマイズしたバージョンとしてMDGRAPEも開発するようになりました。
そうか、基本的には重力問題も、玉とバネのモデルが適用できるんですね。
MDGRAPEとGRAPEは、対象としている現象は違うんだけど、同じ問題を解くための専用コンピューターなんです。
専用マシンと汎用マシン
専用と汎用って何が違うんですか?
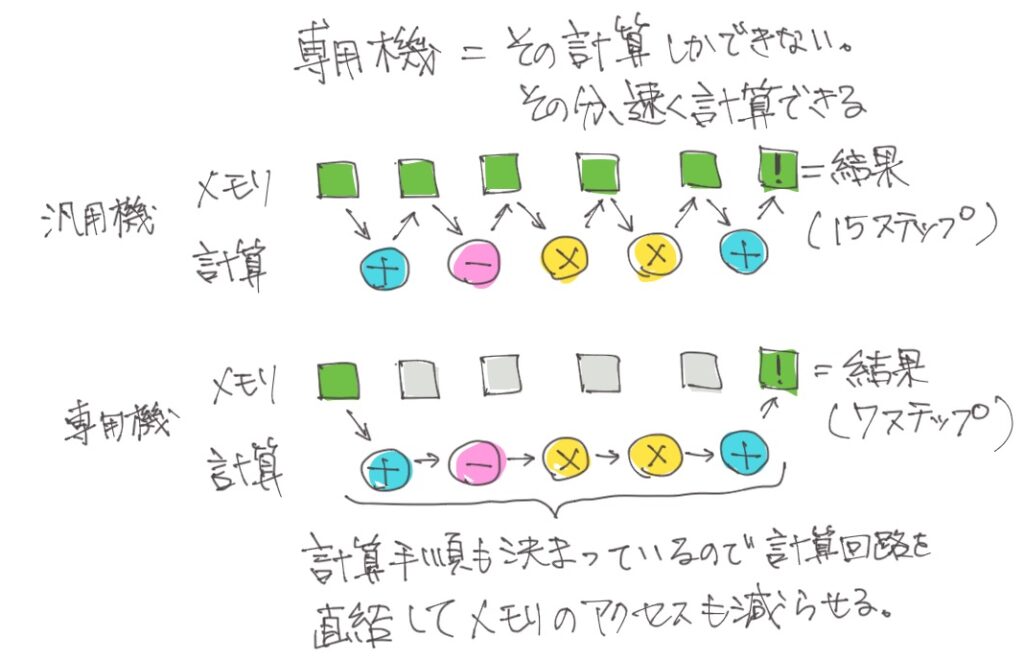
簡単にいえば、専用マシンはある特定の計算に特化していて、他のことをやる能力は削ぎ落としているんです。筋肉質というか。
例えば重力の計算だと、\begin{equation}F = G \frac{m_1 m_2}{r^2} \end{equation} というニュートンの重力の式がありますよね。
コンピュータはこの計算を一つずつやってくわけです。
m1とm2を掛け算して、その距離を2乗して…と言う感じですか?
そうです。先程の銀河に10億個の星がある問題だったら、それを10億×10億回やるわけです。実際には、m1とm2の位置のxyz座標から距離rを割り出す、という計算も入ってきます。
でも、それって汎用マシンでもできますよね?
専用マシンの場合は、この計算のためだけの回路が物理的にチップ上に作られていて、その計算しかできない。そのかわりに、メモリのやり取りを最小化することで計算速度を上げているんです。
とんがってますねぇ。
先ほどの新型コロナのタンパク質のシミュレーションは100万原子くらいなんですけど、こういう計算は「富岳」全体を使ってやっても性能が活かせないんですよ。
世界初のペタフロップスマシン
天文も分子でも、それこそ「天文学的な数」を扱うわけですよね。
組み合わせというところが問題なんですよ。玉の数を増やすと組み合わせは2乗で増えていきます。
めちゃめちゃハイスペックが要求されますね。
でも、全部が全部ハイスペックじゃなくてもいいんです。
どういうことですか?
例えば粒子の数が10倍になると、計算はその組み合わせで計算量は100倍になります。だけど、メモリは粒子の数の情報を保持していればよいだけなので10倍あればいいんです。なので、計算だけ高速化していこうという方針が取れるんです。
そこを極めていって、3号機となるMDGRAPE-3ではコンピュータの計算能力を現す指標の一つであるフロップス(Floating point number Operations Per Second)で世界初のペタフロップスを実現したんです(ペタ=1015、毎秒1000兆回計算ができる)。ただ、専用マシンなので、有名なスーパーコンピュータのベンチマークには載せられなくて、TOP500とかには出てこないんですけどね。でも、理論上の計算能力はこの時点で世界一でした。
そうなんですね!これは、もっと知ってほしい事実ですねぇ。
さらなる高速化を目指して
もっと長い時間のシミュレーションのためには、さらなる高速化が必要なんですよね。
でも実は計算部分じゃないところが問題になってきたりするんです。一つは通信です。計算する部分とメモリの通信がボトルネックになります。
計算量を上げると、通信が追いつかなくなる。一方で、通信が追いつくくらいに問題を小さくしてやると、通信ばかりで計算はほとんどしていない、というような意味のない状態になってしまうんです。
なるほど…。計算だけが速けりゃいいってもんでもないんですね。
一方で、たくさん台数つなげばいいってもんでもない、ということでもあります。この辺りはスケールの仕方の議論になります。
スケールの仕方?
大きく分けるとストロングスケールとウィークスケールという考え方があります。
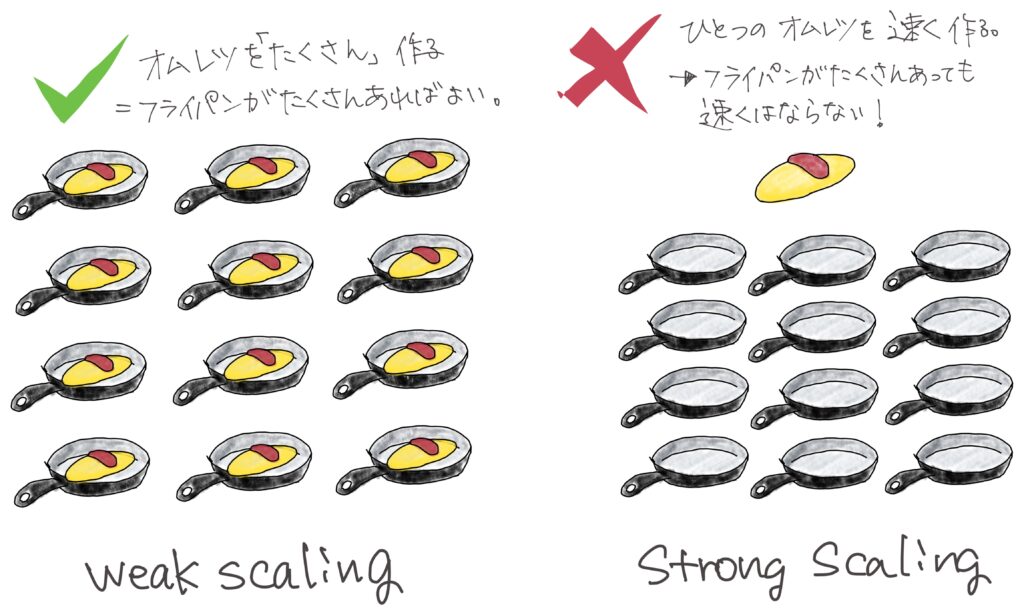
例えば、100人の職人と100個のフライパンがあれば、1個のオムレツを作るのと同じ時間で100個のオムレツができる。これはウィークスケーリングといいます。でも、これだと時間は100分の1にはなりません。
だから1個のオムレツを100分の1の時間で作るにはどうしたらいいか、という問題に対しては違う考え方をしないといけないんです。これがストロングスケーリングです。
あるいは100個のフライパンを持っていても100倍の大きさのオムレツにはならないんです。そのために100倍の大きさのフライパンを作ったときにきちんと動くかどうかというのが、「富岳」みたいなスーパーコンピュータが単純にPCをただつなげただけとは違うところなんです。
MDGRAPEの今後はどうなっていくんですか?
今は計算を少しモジュール的に分割してみたり、アルゴリズムの改良もしながら、次のマシンの設計をしているところです。
やー、勉強になりました!また世界一取ってほしいです!

編集後記
今回の面白いお話を聞いて、MDGRAPEみたいな専用計算機のことがあまり知られていないのは、もったいないなと思いました。実際は専用のチップの製造なども必要で、その辺りの苦労話(小ロット生産がゆえ、とか)もお聞きしたんですが、話がてんこ盛りになったので今回は割愛。残念。
